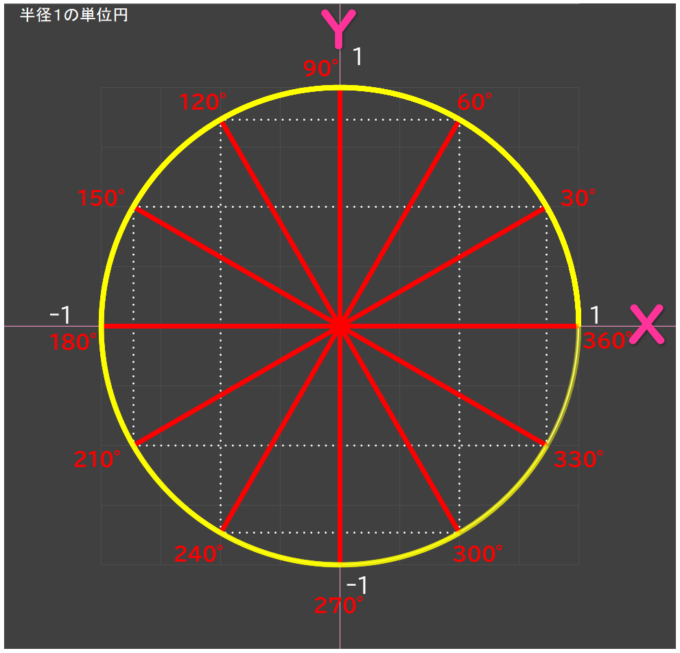
サイン・コサインは、円周上にある点Pの位置。

次の図で、点Pの位置がサイン(sin)とコサイン(cos)。
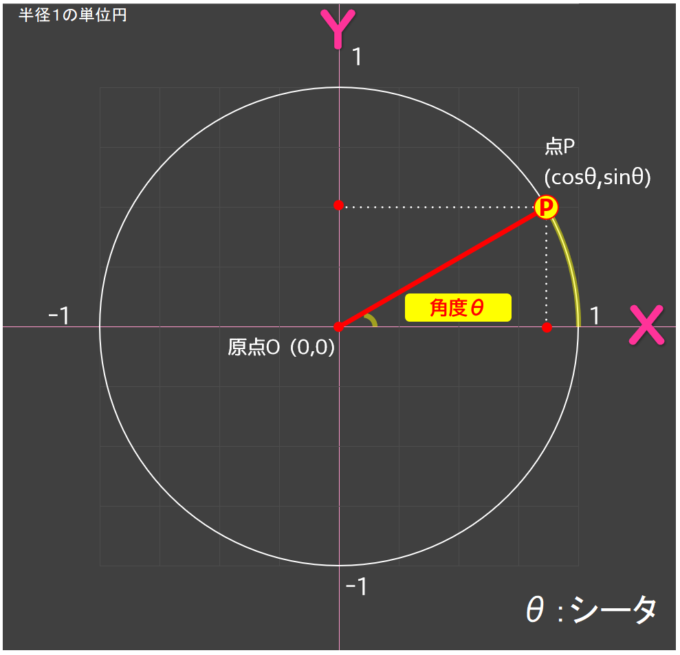
原点(0,0)を中心にした単位円の、円周上にある点の座標を使ってcosθとsinθを決めたということ。よく使うものだから名前を付けたと思ってもいいよ。
(by 数学ガールの秘密のノート 丸い三角関数)

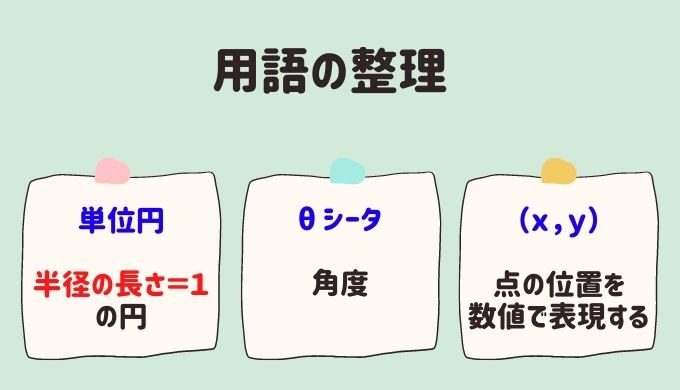
- 「半径の長さ=1」の円を、「単位円」と呼ぶ
- θ(シータ):角度
- cosθ(コサイン・シータ):x座標
- sinθ(サイン・シータ):y座標
- (x,y)が、「点」の位置

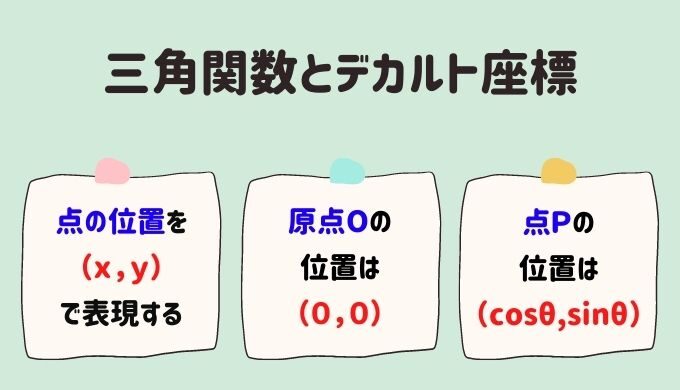
なお、x軸・y軸がある座標を、デカルト座標と呼びます。
デカルトがx軸・y軸を生み出したことで、図形が正確に書けるようになりました。
たとえば、下の図では。

「Y」には縦の棒があるから、「Y=タテ」と覚えよう。

では、点Pが円周上を動くと、y座標の数値はどうなるでしょう?
今回は主に、y=サイン・シータを確認してみます。

sinθ(サインシータ)とは、yの位置のこと

まずは、わかりやすいところから。
サイン90度=1
円の半径の長さを「1」とすると。

これは、わかりやすい。
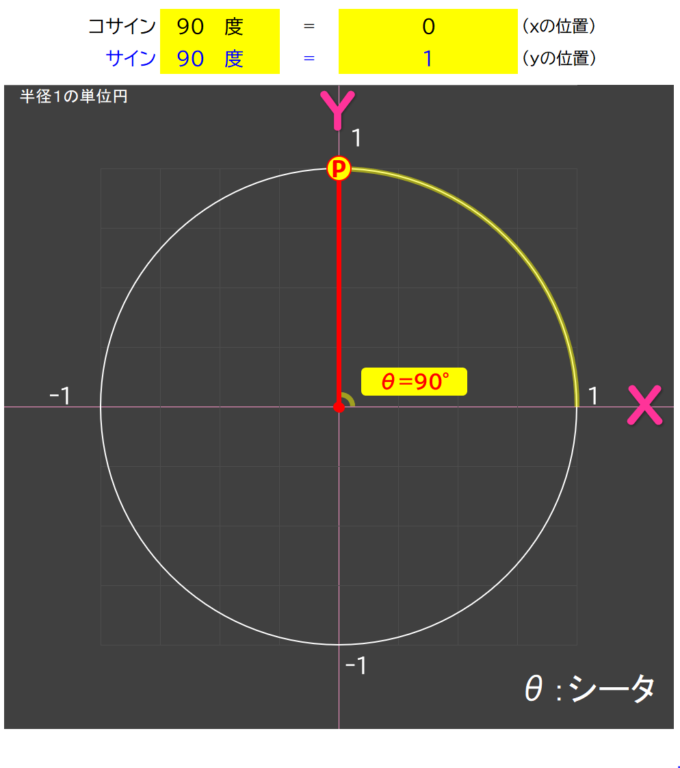
サイン180度=0

出発地点から見て、正反対にきたね。
「0度と対称」になるんだ。
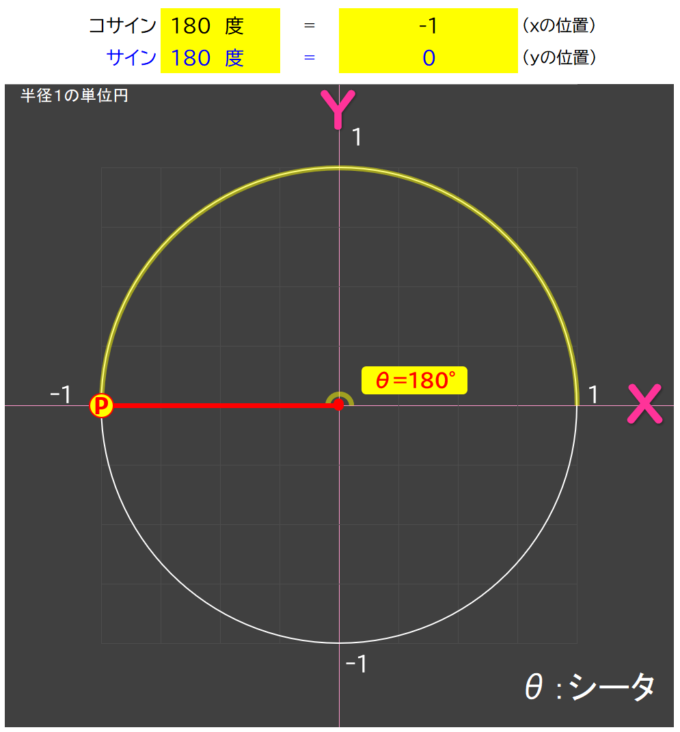
サイン270度=-1

「90度と対称」で、下側だからマイナスになるね。
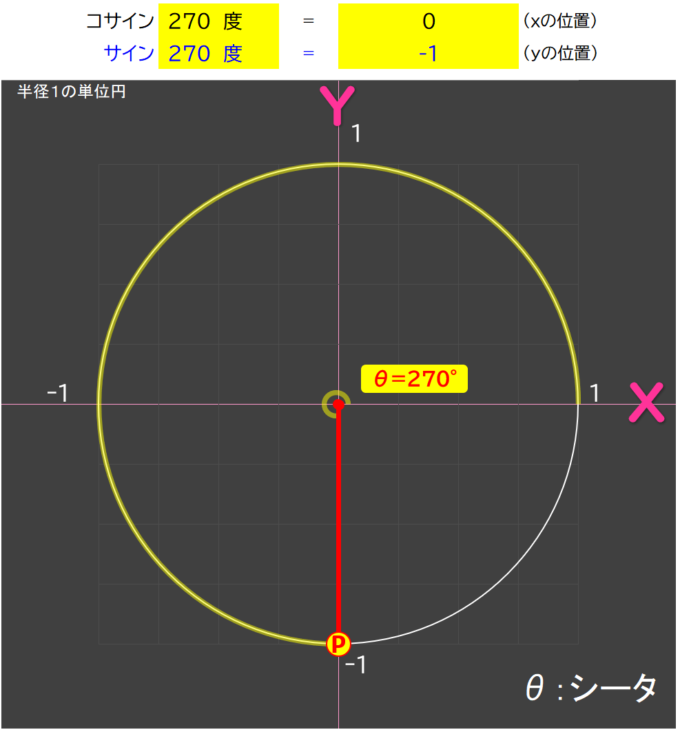
サイン360度=0

ぐるっと一周すると、また0に戻る。
ここまでは、軸を見ただけでも、すぐにわかります。
問題は、それ以外。
ちょっと複雑な計算が必要。
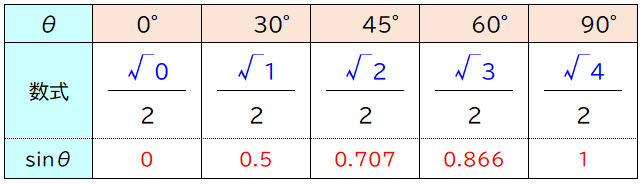
サイン45度=0.7

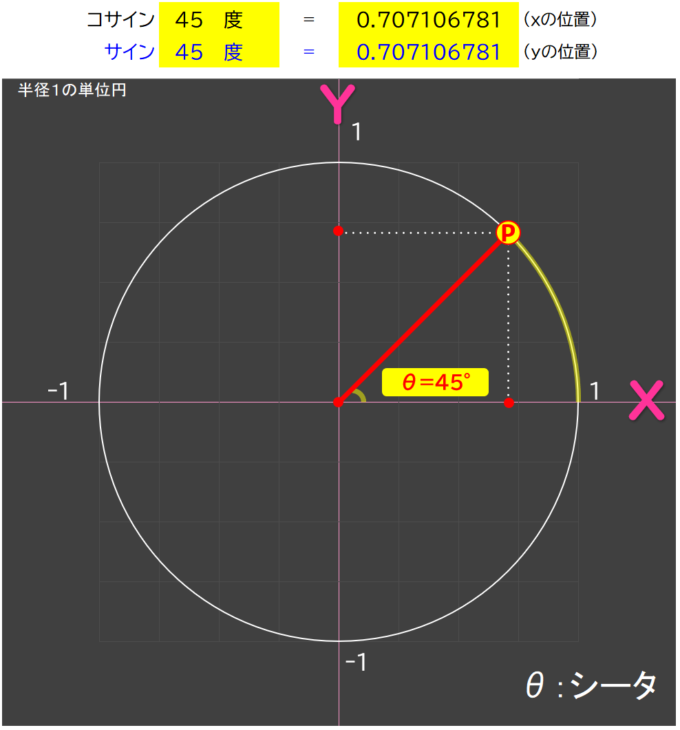
点Pの位置を見ると、「0.5と1の中間くらい」ですね。
ピッタリの数字ではないため、見た目ではわかりません。
ここで登場するのが……
ピタゴラスの定理

これです!
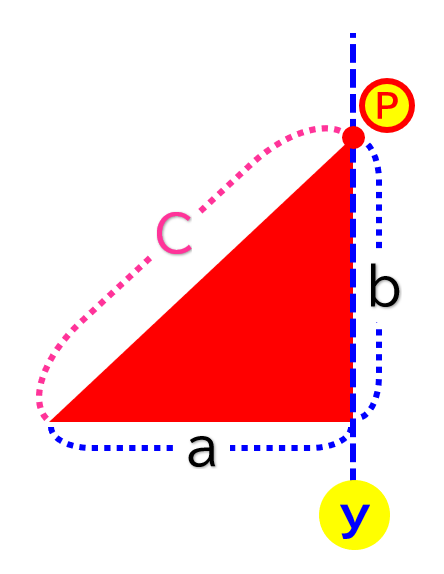
↓ 常にこういう法則になる
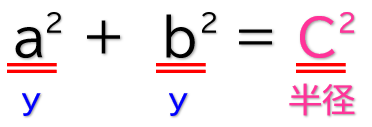
円の中に直角三角形を当てはめると……
- a と b
- = y
- c
- = 半径の長さ
↓ だから、こうなる
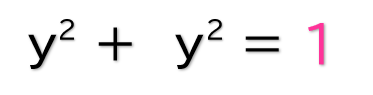
↓ さらに展開を重ねると、こうなる
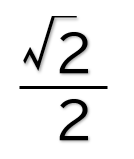
ルート2の覚え方は……
ひと/よ/ひと/よ/に/ひと/み/ご/ろ
つまり。
1.41421356 ÷ 2 = 0.707…

すると、その対称は、とてもラクです。
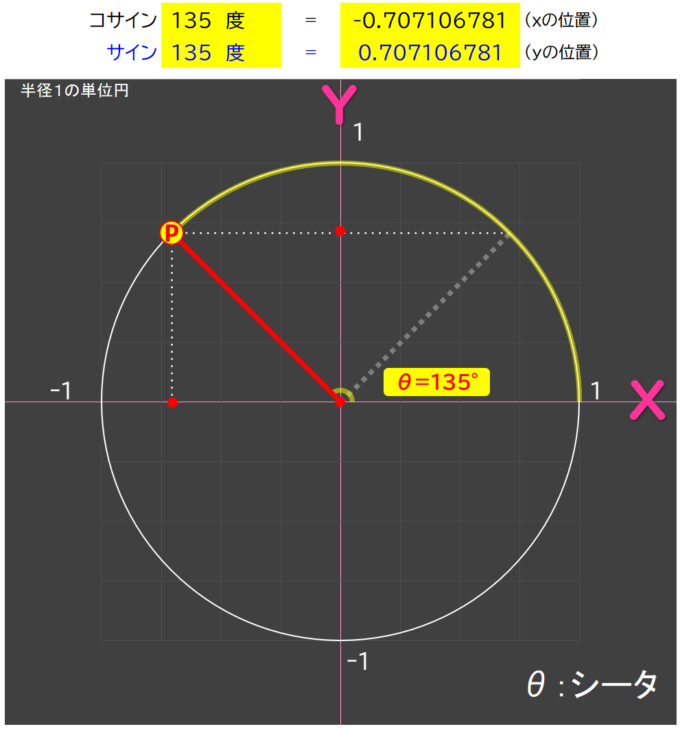
サイン135度=0.7

yの位置は、45度のときと変わらないんだな。
その真下も、ラクです。
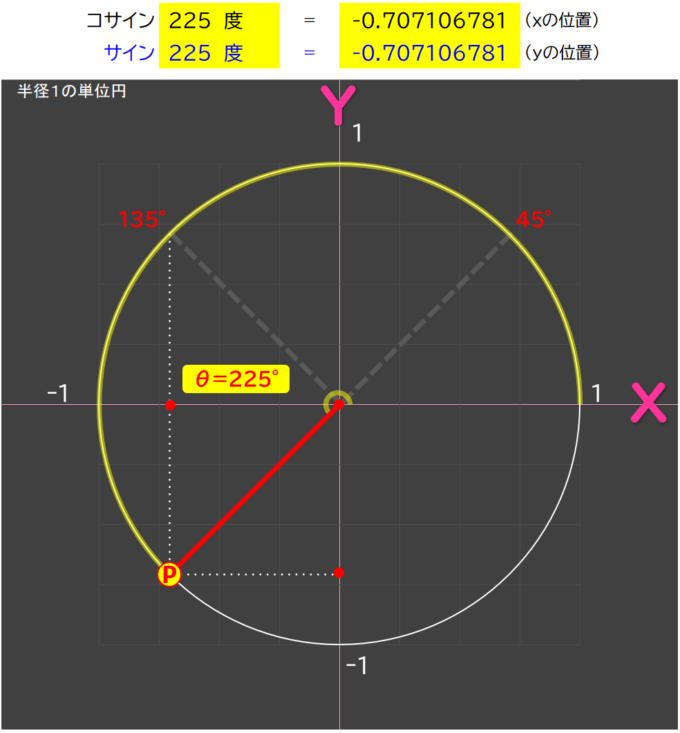
サイン225度=-0.7

下側だからマイナスだ。
すると、その対称も……。
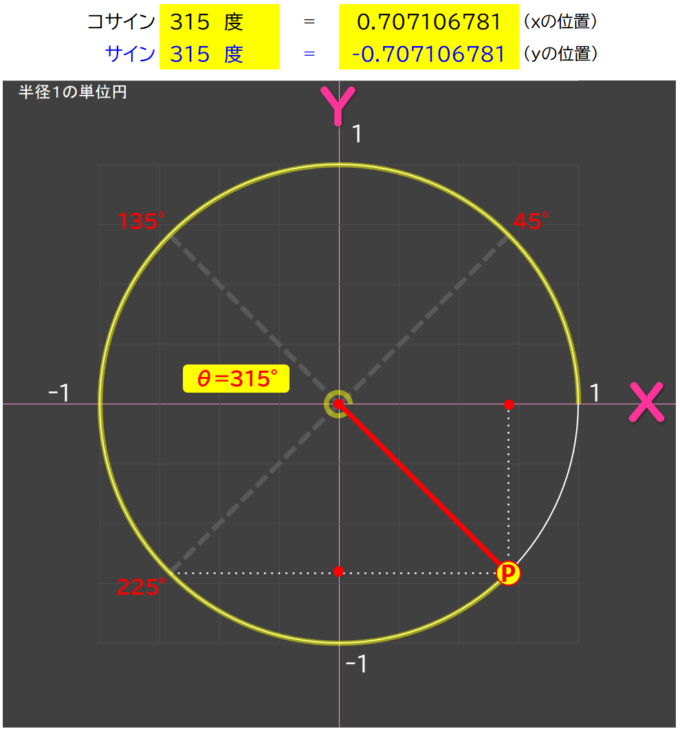
サイン315度=-0.7

yの位置は、225度のときと変わらない。

サインシータのまとめ
円で一周させると、こうなる。

三角関数は円関数といってもいいくらいだと思うな。だって、三角関数は、角度θから、円周上にある点のx座標(cosθ)とy座標(sinθ)を生み出すんだからね。
(by 数学ガールの秘密のノート 丸い三角関数)
ピタゴラスの定理を使って、サイン・シータを計算すると、こう。

数字って、不思議。
90度~180度は対称になるから、yは同じ。
180度~はマイナスすればいい。
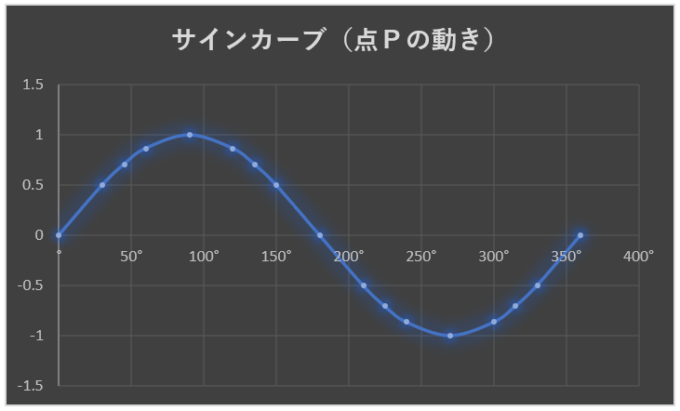
サインカーブ
円周上での点Pの動きを表にするとこう。

エクセル関数
サイン・コサインは、エクセル関数で簡単に計算できます。

一度、「ラジアン」という弧度法に置きかえる必要があります。
サイン・コサインは、ラジアンから計算。
上の例での関数
- =RADIANS(B2)
- =COS(B1)
- =SIN(B1)

結局、サインって何?
円周上における、点Pのy軸の位置。
コサインの場合は、x軸の位置。
コサインがx座標で、サインがy座標。点を回せば角度θ(シータ)が変わって、x座標とy座標もそれぞれ変わる。それだけのことなんだ。
(by 数学ガールの秘密のノート 丸い三角関数)

- 点の位置を、(x,y)の数値で表わす
- 原点Oの位置は、(0,0)
- 点Pの位置は、(cosθ,sinθ)
- θ(シータ)は、角度のこと

x軸とy軸を発明したのは、デカルト。
デカルト座標があるおかげで、私たちは、きれいな図形を描くことが可能になりました。
もちろん、今はエクセルがあるから簡単ですが。
昔の人にとっては、大きな課題だったのです。
きれいな左右対称も描けるし。
円も描ける。
さまざまな数字の不思議も発見され、それによって、数学ひいては文明が大きく前進したそうです。

知らないところで、いろんな人の恩恵を受けて生きているんですよね。
それを垣間見るだけでも、ふだんの何気ないルーチンワークが新鮮に思えてくるかもしれません。
私がこれまでに解決した個々の問題は、後に別の問題を解決するための法則となった
(by デカルト)
デカルトが残してくれた知識を活用し、自分はどんな問題を解決するのか。
「表」と「グラフ」は、どんな仕事をしてても、活用する場面が多いですよね。
エクセルがあれば、特に考えなくてもできることですが。
ちょっと理解しておくと、活用の幅が広がります。
【参考図書】
文系出身者の数学の学び直しには、このシリーズが一番オススメ。






