- 感覚に頼るのではなく、論理に頼る
- 言葉に頼るのではなく、数式に頼る

論理とか数式って、そんなに大事?

自分の言葉を捨てると、逆に言葉が磨かれる
「自分らしく」が大事だと思っていると、とても新鮮な発想だと思います。
数式を大切にすると、感覚がとぎすまされてくる。
そんなことを学んでみたいと思います。
例示は理解の試金石
仮定してから、証明を進める

仮定ってなんだ?

先に結論を考えること
小説の中で、「数学的帰納法」の話が出てきます。
「自然数 k に関して P(k) が成り立つと仮定します……」
そこで後輩が叫ぶ。
そんなやり方、「すっごくおかしいですよ」と。
つまり、こういう疑問。
- 結論を仮定してから始めるって、おかしい
- 話は、前から順番に進めていくものでは?
私は、この「数学的帰納法」の話に、とても感動してしまいました。
「仮定して証明」ってすごいな、と。
普段は、「◯◯だから、こう」「AだからBになる」と考えている。
そこをひっくり返し、「仮に◯◯が成り立つとして……」「Bになったと仮定して……」と、仮置き。
仮置きから話を始める、それが数学的帰納法という手法だそうです。
ひっくり返すと、見えなかったものが見えてくるようになる。

ところで「帰納」ってなんだ?
- 帰納とは
- 具体的な事柄から、法則を導き出すこと
当たり前なことでも、具体例を挙げて考える
「当たり前」も大事だよ。当たり前の例でも、自分で作ってみる。当たり前のことでも、自分で言葉にしてみる。勉強では、そういうのが大事なんだよ。
数学ガール ゲーデルの不完全性定理
人の心は具体例を圧縮する。無意識にパターンを探し、短い表現を見つけるのが人の心だ。
数学ガール ゲーデルの不完全性定理

「1+1=2」は当たり前だ

「当たり前」ではなく、具体的に表現してみよう
「常識を疑う」とは、具体例を挙げること。
丁寧に「仮に……」と考え続けること。
「当たり前」という発想からは、言葉が磨かれないのかもしれません。
「わかるまで」考える
「わかったふり」をしない
しっかり自分の頭で考えるのはとても大事だ。授業が終わってからも、時間をかけて考える。
数学ガール ゲーデルの不完全性定理
決して「わかったふり」はしない。「ここは、まだわかっていない」と意識する。ほんとうに納得するまで考え抜く。真剣にやればやるほど、勉強はおもしろくなる。
数学ガール ゲーデルの不完全性定理

「わかったふり」はしてないつもりだけど

「わかってないところ」は本当にない?
「わかった」と思っても、「わかってない」ところは必ずある。
そう思うと、勉強方法が変わりそうです。
むしろ「まだわかってない」ほうが、いい
わかった気になるよりは、ずっといい。「この数学の本に書かれているのは、こういう意味かもしれない。でも、ほんとうのところは、自分はまだわかっていないかもしれないな」というくらいがいいんだよ。
数学ガール ゲーデルの不完全性定理
- 「わかった」ところを探すより、「まだわかってない」ところを探す

「何がわからないか」が、わからない
「わからなくなる最前線」を探す
たとえば、「数学的帰納法」がわからないとしよう。「自分は、どこがわかってないんだろう」って鏡に向かって――つまり、自分自身に――訊こう。つい「ぜんぶ、わからない!」って言いたくなるけれど、そこで、ぐっと踏ん張る。そして、自分はどこからわからなくなるのか根気よく探す。自分にとっての
「わからなくなる最前線」
を探そう。ここだ!……と最前線が見つかったなら、本屋に来て、参考書を開く。
数学ガール ゲーデルの不完全性定理
- 「何がわからないのか」を自分で考える
- 「わからなくなる最前線」が見つかるまで探す
- 見つかったら、何かに頼る(本で調べる、人に聞く)

わからなくなる最前線って?

それは絶対に、自分にしかわからないこと
「わからなくなる最前線」は、人それぞれ違うもの。
だから、絶対に他人にはわからない。
自分が見つけるしかない。
- 自分で考える
- なぜなら、疑問も答えも自分の中にしかないから
「いや、自分はわかってない」と言う勇気をもつ
たとえ、世界中の人が「わかった、簡単だよ」と言ったとしても、自分がわかっていなかったら「いや、自分はわかっていない」と言う勇気。それが大切なんだ。他人がいくらわかっても、自分がわからなければ無意味。時間をかけて考える。納得するまで考える。そうして得たものは、一生、自分のもの。決して誰にも奪われない。真剣な勉強をていねいに積み重ねていくことが、自信につながる。
数学ガール ゲーデルの不完全性定理

早くわかるようになりたいけど

時間をかけたほうが、自分のものになる
なぜ勉強するかといえば、わからないから。
でも本当は、わからないところを考えること自体が楽しいのかもしれません。
誰もが、想像を絶する道のりを通る
急ぐ必要はないよ。だって、数学が現在の形になるまで、何百年も何千年もかかっているんだよ。各時代の最高の頭脳が知恵をしぼりにしぼって……。いま数学の本に載っている記号や、数式や、考え方が生まれるまでには、想像を絶する道のりがあったはずなんだ。だから、見てすぐわからなくてもいいんだよ。
数学ガール ゲーデルの不完全性定理

数学は、パパっと計算するものだと思ってた

数式を解いていくことは、誰でも時間がかかる
なんでも早く・効率的に過ぎていく世の中だから。
むしろ、難しい数式とじっくり向き合うことが、ぜいたくな時間になるのかもしれません。
気難しくて暗いイメージだった数学が、新鮮に思えてきます。
「分けて」考える
分けることは、分かることへの第一歩
複雑な式を読むとき、全体をいっぺんに理解しなきゃと思っちゃだめ。複雑な式も、部分部分は簡単だ。だから、分けて考えよう。分けることは、分かることへの第一歩。
数学ガール ゲーデルの不完全性定理

部分は簡単?

「分ける = 分かる」と思うと、安心できますね
- 複雑な式は分けて考える
- ギリシア文字が出てきてもあわてない
- 変数の意味を考える
- 絶対値の意味を考える
- 図で表してみる
- 不等号の意味を考える
分けてみれば、見えてくる。
「場合分け」という言葉も、数学ではよく出てきます。
「こういう場合ならどうか?」「では、これは?」と。

分けたあとは、どうするの?

分けただけでは、ダメなようです
部分を見たあとは、全体の構造を見る
(部分しか見ないのは)美しいパターンを描くレース模様を見て、「穴が空いているのもいいものだ」というのと似ている。レース模様のパターンが生み出しているものは何かを理解していない。世界を表面だけ観察している。構造を見抜いていない。もっと深い楽しみがあるのに……。
数学ガール ゲーデルの不完全性定理
自分が関心のある理論は、どんな構造を持つのか。複数の理論の間には、どんな関係があるのか。……それはとても深い楽しみを生み出す問題のはずなのに。
数学ガール ゲーデルの不完全性定理

構造?

部分が集まって全体が成り立っていること
部分と部分は、孤立しているのではなく、集まって全体を作っている。
部分が集まるときには、規則的なパターンがあります。
ただの一つの穴が、集まってレース模様になるように。
穴とレース模様の関係という「関係性」「パターン」を見ることが、構造を考えること。

でも、それにどんな意味があるの?
「意味」は考えない
意味ではなく、形に注目する
人間が意味を考えた上で論証すると、根拠が不明確になることがある。一方、意味を考えず、形だけに注目するなら、根拠が明確になる。何しろ、明確に定義されたことだけを用いるから。
数学ガール ゲーデルの不完全性定理

意味を考えないの?

感情よりも、定義を大切に
「意味を考えない」とは、ちょっと衝撃かもしれません。
でも、意味を考え始めると、自分の感情が中心になってしまう。
そうではなく、しっかりと形を見つめて、定義を明確にして、構造を把握する。
実はそのほうが、大事なことに集中できるようです。

大事なことに集中する?
思考を、機械的な計算でおこなう
ライプニッツはね、「思考」を「計算」に見立てたんだ。論理的な思考を、機械的な計算で行おうと考えた。
数学ガール ゲーデルの不完全性定理
人は誰でも計算だけで、現に最も困難な真理すら判断することになるであろう。以後、人々は、すでに手中にしているものについて、もはや論争することなく、新たな発見に向かうことになろう。
by ライプニッツ

計算で動くなんて、打算的じゃないの?

いちばん大事なことにだけ、頭を使えばいい
すべてのことを人的な作業にすると、とてもストレスがかかります。
脳の処理能力を、必要以上に使ってしまうからです。
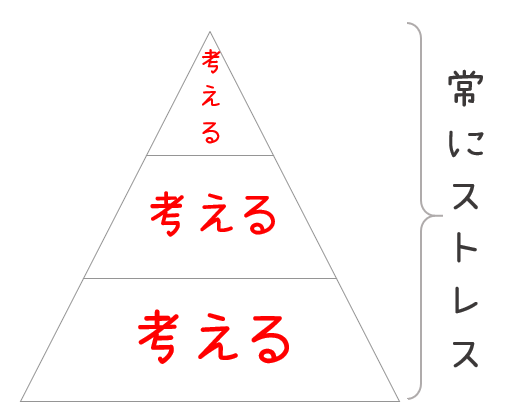
これを、機械的な計算に頼るようにすると……
↓
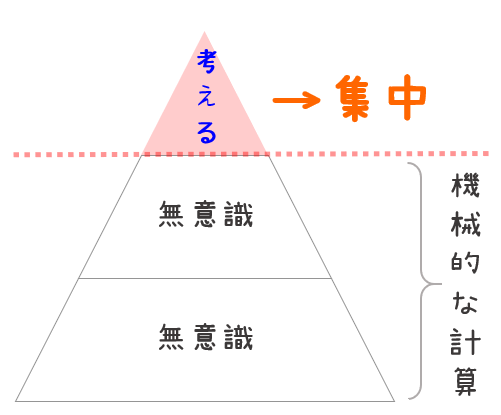
やる気が出ないのは、大事なことにたどり着く前に、脳を使い果たしてしまうからかもしれません。
どうでもいいことに、感情が振り回されてしまうからですね。
意味を考えず、計算に身をまかせる
問題を読んで式を立てた後は機械的計算――意味を考えないでも進められる計算――に身をまかせる練習なんだよね。まず具体例で問題を理解することは大事だけれど、どこかの段階では、「意味の世界」から「数式の世界」へ考えを移す必要がある。式を立てる、ってそういうことだよ。「数式の世界」に行きさえすれば、意味を考えなくても式変形ができる。方程式のいろんな解法が使える。最後に得られた結果を「数式の世界」から「意味の世界」に戻せば、もとの問題が解けていることになる。
数学ガール ゲーデルの不完全性定理

「意味の世界」から「数式の世界」へ?

最後に、「意味」に戻ってみる
- 具体例で考える
- 「意味の世界」から「数式の世界」へ
- 式を立てる
- 意味ではなく、純真に形だけを見る
- 「数式の世界」から「意味の世界」へ
- もとの問題は解けている

たしかに、意味ばかり考えて動けなくなることが多い

いちど意味を捨てたほうが、早く意味にたどり着けるのかも
螺旋が意味するもの
落ち込むな。落ち込むな。落ち込む自分に酔うな。
きみには――すべての次元が見えているのかな。
きみには、円周を回る点しか見えてない。
きみには、螺旋が見えてない。
数学ガール ゲーデルの不完全性定理
同じように見えるけれど、単なるループではない。
繰り返しながら昇っていく――螺旋だ。
数学ガール ゲーデルの不完全性定理

螺旋が見えてない?

繰り返しに見えて、実は昇ってる
「悪循環」といいますが、実は「循環」はしていないのかもしれません。
同じ状態に戻っているのではなく、上へ昇っている。

螺旋の道を歩いているのかな

形に注目すればわかるかも
海に注いで川は終わる。
でも、水の旅がそこで終わるわけじゃない。
そこから水は、天へ昇るのだ。
数学ガール ゲーデルの不完全性定理





まとめ
有名な論法でも、きちんと理解しているかどうかを確かめるのは大切なことなんだな。「名前を聞いたことがある」や「本で読んだことがある」というレベルと、「きちんと理解している」というレベルの間には、すごく大きなギャップがありそうだ。
数学ガール ゲーデルの不完全性定理
いわば「数式の世界」は、この世を映し出す鏡のようなものだよ。うまく映してやると、数式の変形で、この世の問題を解くことができる。
数学ガール ゲーデルの不完全性定理
- 例示は理解の試金石
- 仮定してから、証明を進める
- 当たり前のことも、丁寧に考える
- 分かるまで考える
- 「わかったふり」はしない
- 「わからなくなる最前線」を見つける
- 「自分はわかってない」と言う勇気を持つ
- 分けて考える
- 分ければ、分かる
- 複雑な式は、分けてみる
- 部分を見たあとは、全体の構造を見る
- 意味を考えない
- 機械的な計算にまかせる
- 意味の世界から数式の世界へ
- 循環ではなく、螺旋
- 単なるループではない

意味を考えないのは驚きだった

考えないほうが、考えられるようになる



