
ベクトルって何だっけ?
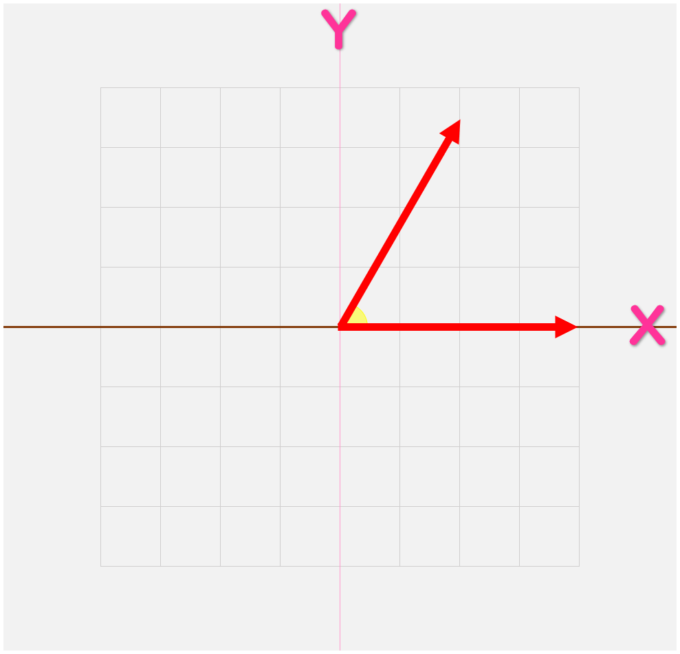

ベクトルには「角度」があるけど、「形」はない
力は数そのものじゃない。でも、数のように計算できるものだよ。
数学ガールの秘密ノート/ベクトルの真実
ベクトルとは
「向き」と「大きさ」がある
向きと大きさがあるものは、ベクトルで表せる。そしてベクトル同士を足すこともできる。
数学ガール ベクトルの真実

「向き」と「大きさ」?

たとえば人が立っているときには「下向き」の力が働いている
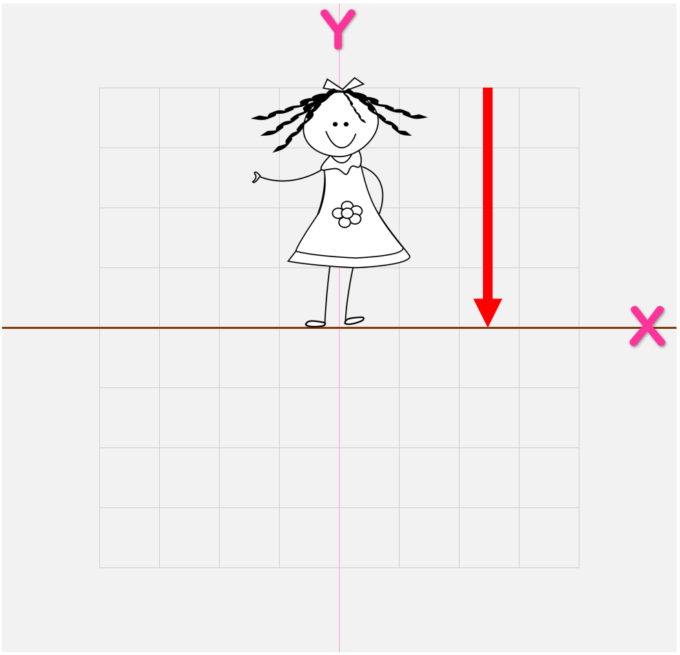

でも、「下向き」だけでは立っていられない
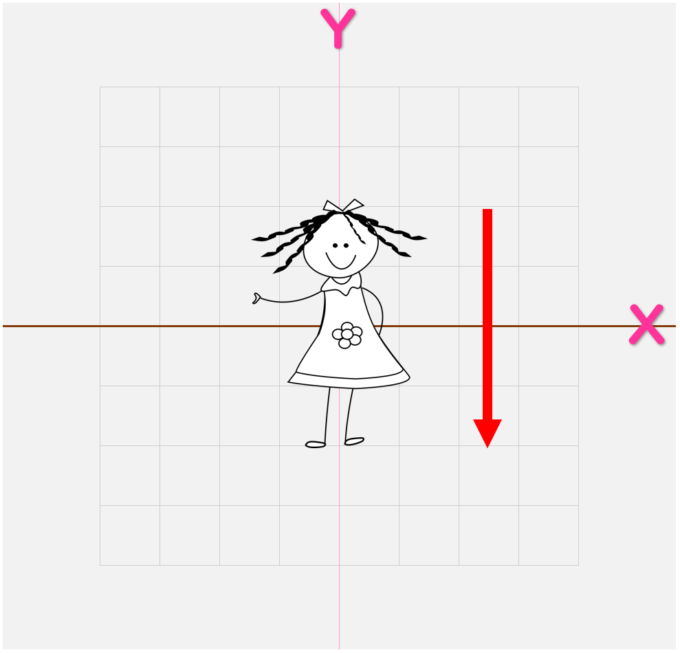

どんどん下にいっちゃうの?
ベクトルは複数ある

ベクトルは1つだけじゃない
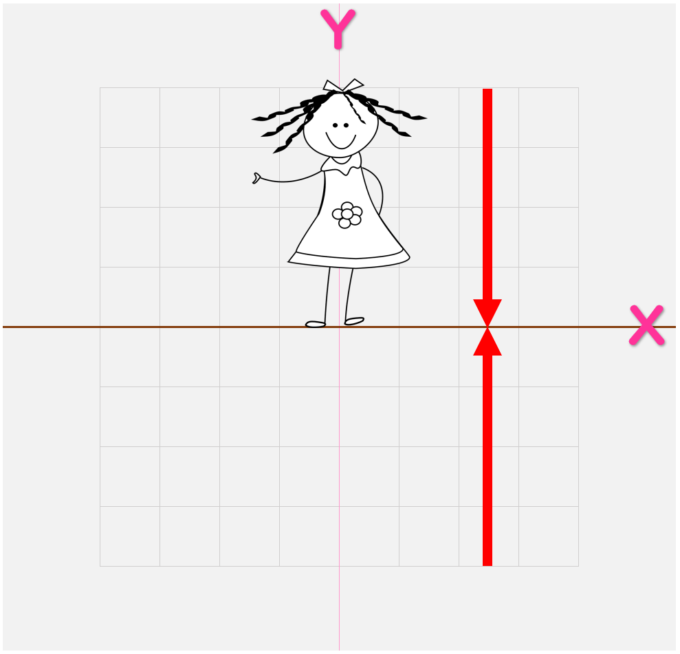

上向きの力もあるんだ
- ベクトルが複数あるから、ベクトルの足し算や、かけ算ができる

何かを持つことができるのも、上向きと下向きがあるから
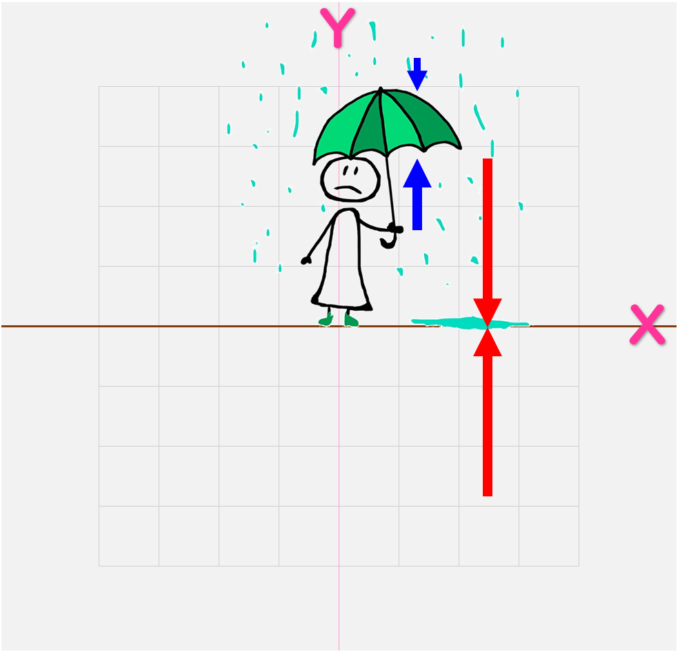
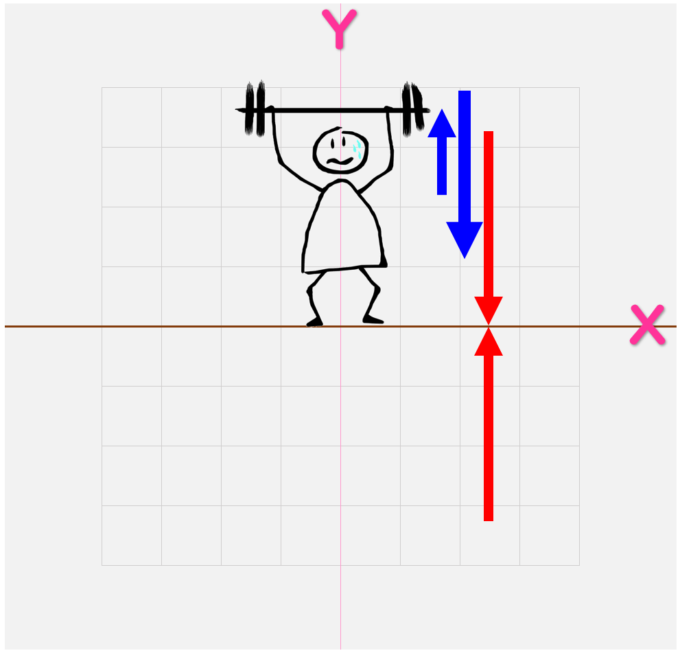
- 「働いている力」を、すべて見つける
- 「どこから・どこへ」向かってるかをハッキリさせる
数字にも、「向き」と「大きさ」がある

数字にも「向き」がある
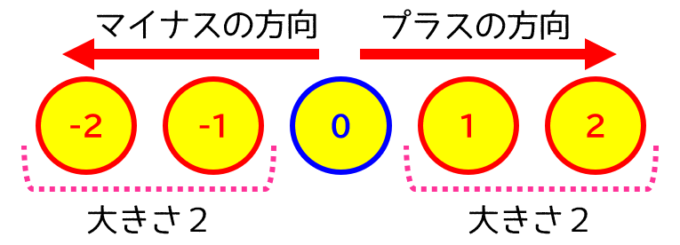

プラスとマイナスは、「向き」なんだ

「大きさ」は、「絶対値」と呼ばれる

じゃあ「数字」と「ベクトル」は何が違う?
ベクトルにあって、数字にないもの
数はプラスとマイナスの2つの向きしかないけれど、ベクトルのほうは数よりもたくさんの向きがあるね。
数学ガール ベクトルの真実

たくさんの「向き」?

「向き」が変わると、「角度」が変わる
角度

ベクトル:形の計算ができる

「円」とか「三角形」とか?

「サイン」や「コサイン」と呼ばれる
数字:数や大きさを表現する
数は言葉みたいなものだね。表現するために使うもの。
数学ガール ベクトルの真実

表現する?
- 個数を数えたいとき
- 温度を調べたいとき
- 重さを量りたいとき
- 力の大きさを表現したいとき

「個数そのもの」「温度そのもの」は、「数字」ではない
数字には形がない。
ある何かを、数字で表現したにすぎない。
数字を使えば、計算ができる。
自分の勉強として、数学をやる
本屋で数学の本を買って読む。放課後に数式をいじる。それは、自分がやりたいことだから。好きなことだから。自分の勉強って、そういうこと。
数学ガール ベクトルの真実
たとえば、「この式がこうなるのはどうしてだろう」って疑問に思うこと、あるよね。
そういうときに「まあいいか、時間もないから覚えちゃえ」じゃなくて、もっとじっくり「どうしてだろう、どうしてだろう」と考える。それは数学が好きだから。それに、理由がわからないと気持ちが悪いから。
数学ガール ベクトルの真実
やっぱり自分で考えて考えて考えなくちゃだめかな。自分なりの納得の仕方というのがあるみたいなんだよ。完全なまちがいは「それは違うよ」と先生が教えてくれるかもしれないけど、「そういうことか!」と納得する最後のステップは、必ず自分の中にある。先生の話はきっかけにすぎなくて。
数学ガール ベクトルの真実
まとめ
- ベクトルの向き
- 角度(いろんな向きがある)
- 数字の向き
- プラスとマイナスの2方向のみ
- ベクトルを考えるときは……
- 「働いている力」を、すべて見つける
- 「どこから・どこへ」向かってるかをハッキリさせる

いろんな「向き」があることと、「大きさ」



